AI：空间可分离卷积，spatial separable convolutions

文章来自微信公众号“科文路”，欢迎关注、互动。转发须注明出处。

AI：空间可分离卷积，，Spatial separable convolutions

上周四介绍了《经典卷积，Normal_convolution》，卷积操作为多维数据的特征提取提供了崭新的方向，也由此诞生了诸多的好成果。但繁重的乘加运算给该算法的普及增添了难度。

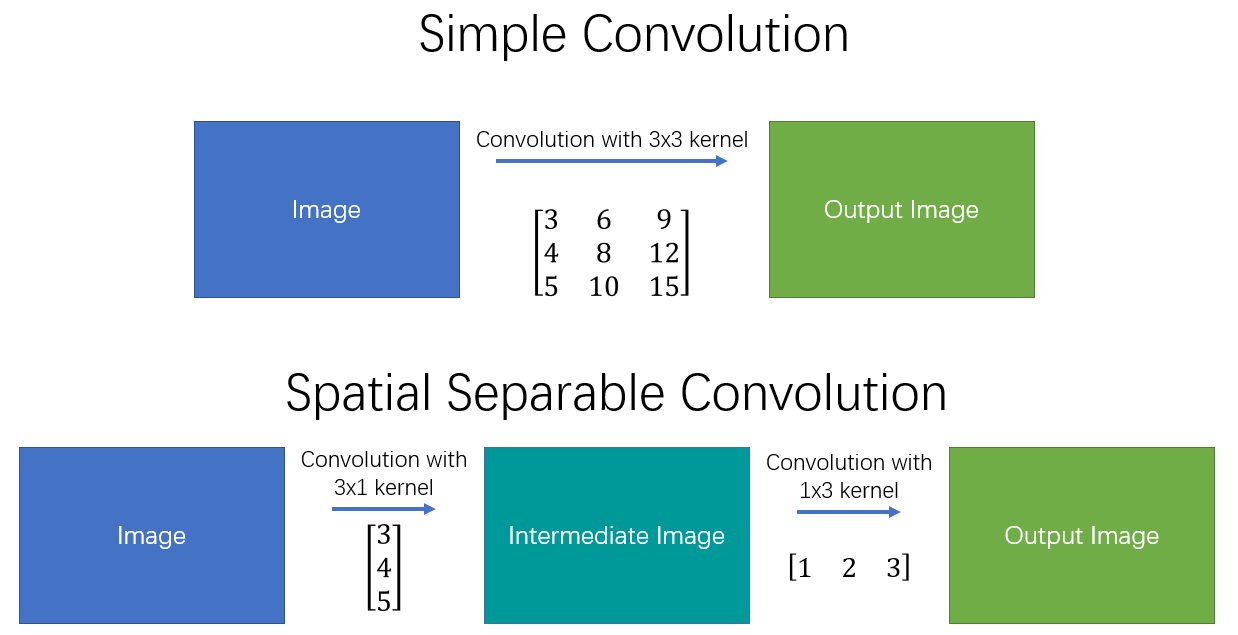
今天介绍经典卷积在计算上的第一种优化，空间可分离卷积。通过讲卷积核拆分成一个列向量、一个横向量分别计算，就可以在比较少的损失情况下，降低计算成本。

我们通过一个例子来看一下。

比如，我们要对一副 $6\times 6$ 图像 a 用 $3\times 3$ 的 Sobel 卷积核 b 做卷积计算（valid, 不padding不pooling）。下面是用 Octave 做的验证。

>> a = [0, 0, 0, 0, 1, 0; 0, 0, 0, 1, 0, 0; 0, 0, 1, 0, 0, 0; 0, 1, 0, 0, 0, 0; 1, 0, 0, 0, 0, 0; 0, 0, 0, 0, 1, 0]

a =

   0   0   0   0   1   0
   0   0   0   1   0   0
   0   0   1   0   0   0
   0   1   0   0   0   0
   1   0   0   0   0   0
   0   0   0   0   1   0

>> b = [-1, 0, 1; -2, 0, 2; -1, 0, 1]

b =

  -1   0   1
  -2   0   2
  -1   0   1

>> conv2(a, b, "valid")
ans =

  -1  -2   0   2
  -2   0   2   1
   0   2   1   0
   2   1  -1   0

>> b_1 = [1; 2; 1]

b_1 =

   1
   2
   1

>> b_2 = [-1 0 1]

b_2 =

  -1   0   1

>> b_1 * b_2
ans =

  -1   0   1
  -2   0   2
  -1   0   1

>> conv2(conv2(a, b_1, "valid"), b_2, "valid")
ans =

  -1  -2   0   2
  -2   0   2   1
   0   2   1   0
   2   1  -1   0

我们通过把 Sobel 算子拆分成两个向量，减少了计算量的同时得到了相同的结果。下面这个图

计算量分析：

• 经典卷积 $3\times 3$ 游走全图 $6\times 6$，每次做 9 次乘法，共做 $4\times 4$ 次，共计 $4 \times 4 \times 9 = 144$
• 空间可分离卷积有先后关系，列向量游走 $6\times 4$ 次，每次做 $3$ 次乘法；横向量在列向量的输出 $4\times 6$ 上游走 $4\times 4$ 次，每次做 $3$ 次乘法，两个向量共计 $6 \times 4 \times 3 + 4\times 4\times 3 = 120$

显然，空间可分离卷积有个很大的问题：并不是所有 kernel 都能被拆成 2 个向量 kernel。关于这个问题，我们下周四继续介绍。

都看到这儿了，不如关注每日推送的“科文路”、互动起来~

至少点个赞再走吧~