科技：卡尔曼滤波器

已收录至https://zhuanlan.zhihu.com/p/52815498

本文内容来自官方教程

可以直接跳到6看

0 例

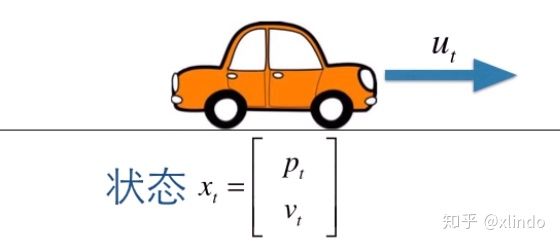
可以列出模型
$$\begin{cases} p_t = p_{t-1}+ v_{t-1} \times \Delta t+u_t\times\frac{\Delta t^2}{2} \ v_t=v_{t-1}+u_t\times\Delta t\end{cases} $$
则可以写出状态空间方程
$$\left[\begin{matrix}p_t \ v_t\end{matrix}\right]=\left[\begin{matrix}1 & \Delta t \ 0 & 1\end{matrix}\right]\left[\begin{matrix}p_{t-1} \ v_{t-1}\end{matrix}\right]+\left[\begin{matrix}\frac{\Delta t^2}{2} \ \Delta t\end{matrix}\right]u_t $$

1 状态预测公式

令
$$F_t=\left[\begin{matrix}1 & \Delta t \ 0 & 1\end{matrix}\right],B_t=\left[\begin{matrix}\frac{\Delta t^2}{2} \ \Delta t\end{matrix}\right], $$
即得出第一个卡尔曼滤波器公式，状态预测公式
$$\displaystyle \hat{x}t^- = F_t\hat{x}{t-1}+B_tu_t \ $$
其中$F_t$状态转移矩阵：从上一时刻推测这一时刻；
$B_t$为控制矩阵：控制量$u$如何作用；
$\hat{x}_t$为估计值；
$\hat{x}_t^-$为未修正的估计值。

2 不同时刻的不确定性的传递关系公式

协方差矩阵

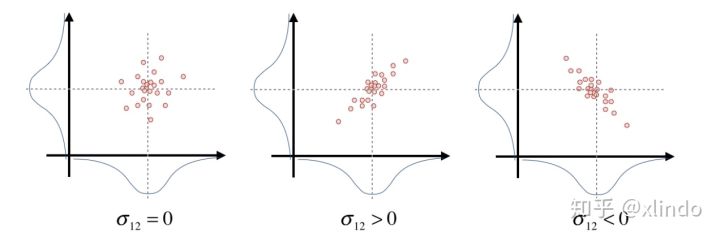
$$
\displaystyle cov(x,x)=\left[\begin{matrix}\sigma_{11} & \sigma_{12} \\sigma_{12} & \sigma_{22}\end{matrix}\right] \ $$
该例中每一个时刻的不确定性都由协方差矩阵$P$来表示，而不确定性的不同时刻传递为 $$\displaystyle P_t^- = FP_{t-1}^-F^T \$$
再加上预测模型本身的状态转移噪声协方差矩阵 Q ，得到第二个公式，不确定性的传递关系
$$\displaystyle P_t^- = FP_{t-1}^-F^T +Q\ $$

3 状态观测

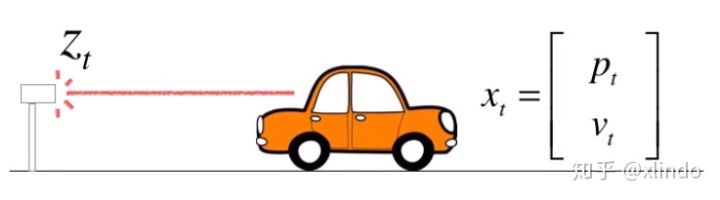
有测量值$z_t$，为一维向量，并加上噪声$v$ ，观测噪声的协方差矩阵为$R$，本例为$R^1$
$$\displaystyle H=[\begin{matrix}1&0\end{matrix}] \ z_t = Hx_t+v\ $$

4 状态更新

实际观测值与预期观测值的残差乘以$K$作修正
$$\displaystyle \hat{x}_t = \hat{x}_t^-+K_t(z_t-H \hat{x}_t^-)\ $$
其中$K$为卡尔曼系数，
$$\displaystyle K_t = P_t^-H^T(HP_t^-H^T+R)^{-1}\$$
其作用为

• 权衡预测协方差$P$和观察两协方差$R$：
  • 若相信预测多一点，则残差权重小一点；
  • 若相信观察多一点，则残差权重大一点。
• 把残差的形式从观察域转换到状态域：$z$为一维向量，而$x$为二维向量，即可以在两个维度同时修正。

5 噪声协方差矩阵的更新

更新最佳估计值的噪声分布 $$\displaystyle P_t = (I-K_tH)P_t^-\ $$
在不确定性的变化中找一种平衡。

6 5个公式

预测：
$$\displaystyle \hat{x}t^- = F_t\hat{x}{t-1}+B_tu_t \P_t^- = FP_{t-1}^-F^T +Q\ $$
更新：
$$\displaystyle \begin{aligned} K_t& = P_t^-H^T(HP_t^-H^T+R)^{-1}\\hat{x}_t& = \hat{x}_t^-+K_t(z_t-H \hat{x}_t^-)\ P_t& = (I-K_tH)P_t^- \end{aligned}\ $$
$x_t$ : t 时刻的状态
^: 观测值
$^-$: 未修正值
$F_t$ : 状态转移矩阵，和具体的线性系统相关
$u_t$ : K时刻外界对系统的作用
$B$ : 输入控制矩阵，外界的影响如何转化为对状态的影响
$P$ : 误差矩阵
$Q$ : 预测噪声协方差矩阵
$R$ : 测量噪声协方差矩阵
$H$ : 观测矩阵
$K_t$ : t 时刻的kalman增益
$z_t$ : t 时刻的观测值

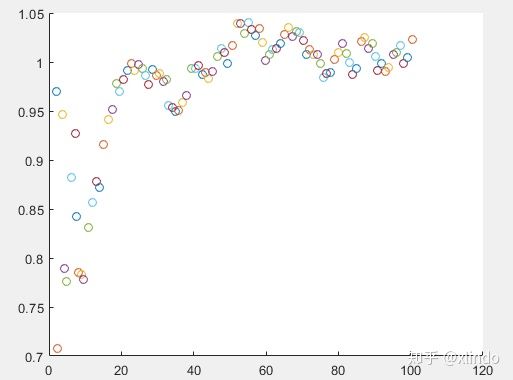
7 Matlab实例

Z=(1:100); %观测值
noise=randn(1,100); %方差为1的高斯噪声
Z=Z+noise;

X=[0; 0]; %状态
P=[1 0; 0 1]; %状态协方差矩阵
F=[1 1; 0 1]; %状态转移矩阵
Q=[0.0001, 0; 0 0.0001]; %状态转移噪声协方差矩阵
H=[1 0]; %观测矩阵
R=1; %观测噪声方差

figure;
hold on
for i=1:100

  X_ = F*X;
  P_ = F*P*F'+Q;
  K = P_*H'/(H*P_*H'+R);
  X = X_+K*(Z(i)-H*X_);
  P = (eye(2)-K*H)*P_;
  plot(X(1),X(2),'o'); %画点，横轴表示位置，纵轴表示速度
end
hold off;

结果如下，