时频分析——短时傅里叶变换STFT
文章来自微信公众号“科文路”,欢迎关注、互动。转发须注明出处。
短时傅里叶变换STFT,在语音识别中有重要应用,这是一篇讲 STFT 的好文。
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
1. 引言
在信号分析中,傅里叶变换可称得上是神器。但在实际应用中,人们发现它还是存在一些不可忽视的缺陷。
为了便于叙述考察以下两种情形:
Case 1
考察这样一个函数:
1 | fs = 1000; |
绘制这个函数的时域图像和经过傅立叶变换后的频谱图像,长这个样子:
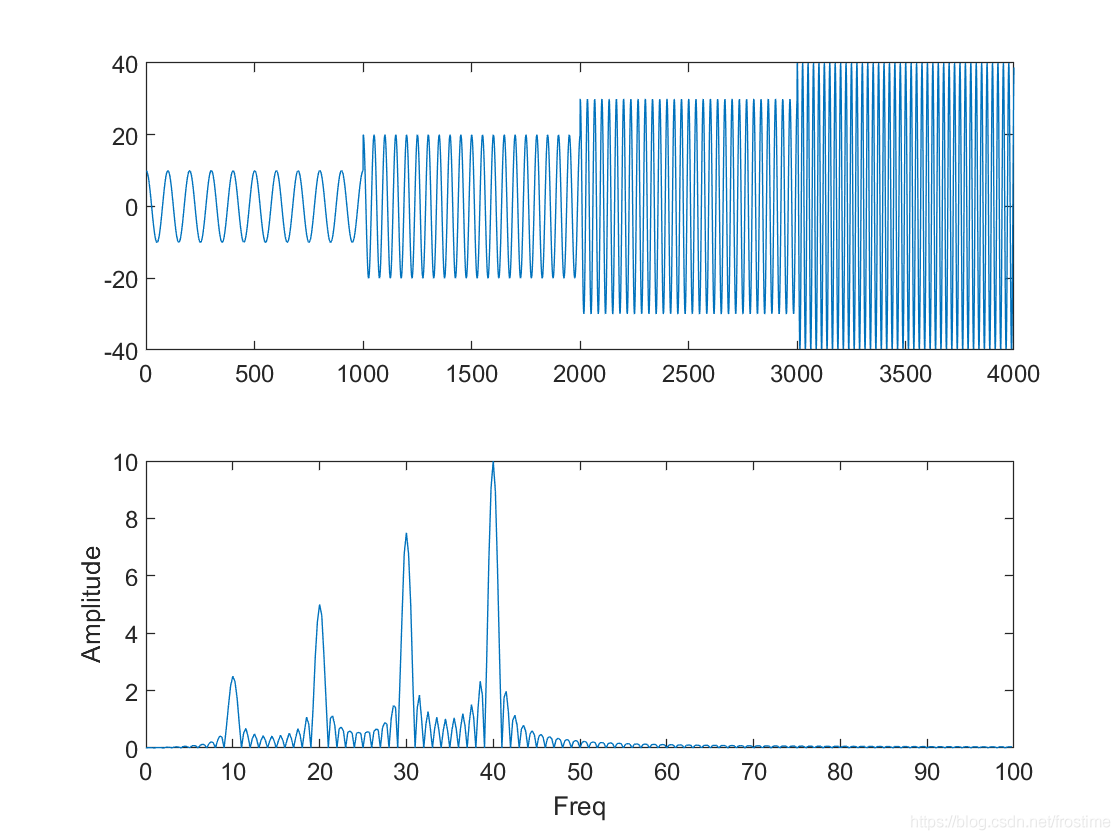
现在把信号反转过来:
1 | x = [10 * cos(2 * pi * 10 * t), 20 * cos(2 * pi * 20 * t),... |
再次绘制时域和频域的图像,它长这样:
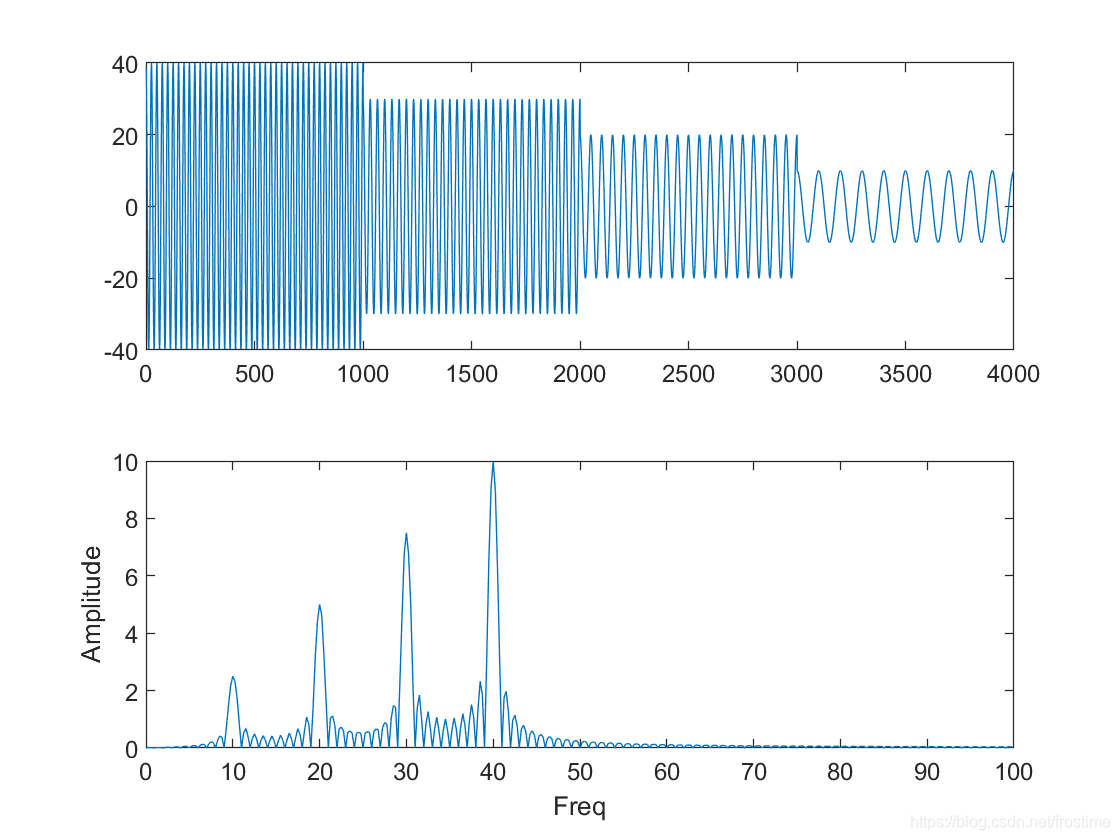
不难发现,尽管这两个信号的时域分布完全相反,但是它们的频谱图是完全一致的。显然,FFT 无法捕捉到信号在时域分布上的不同。
Case 2
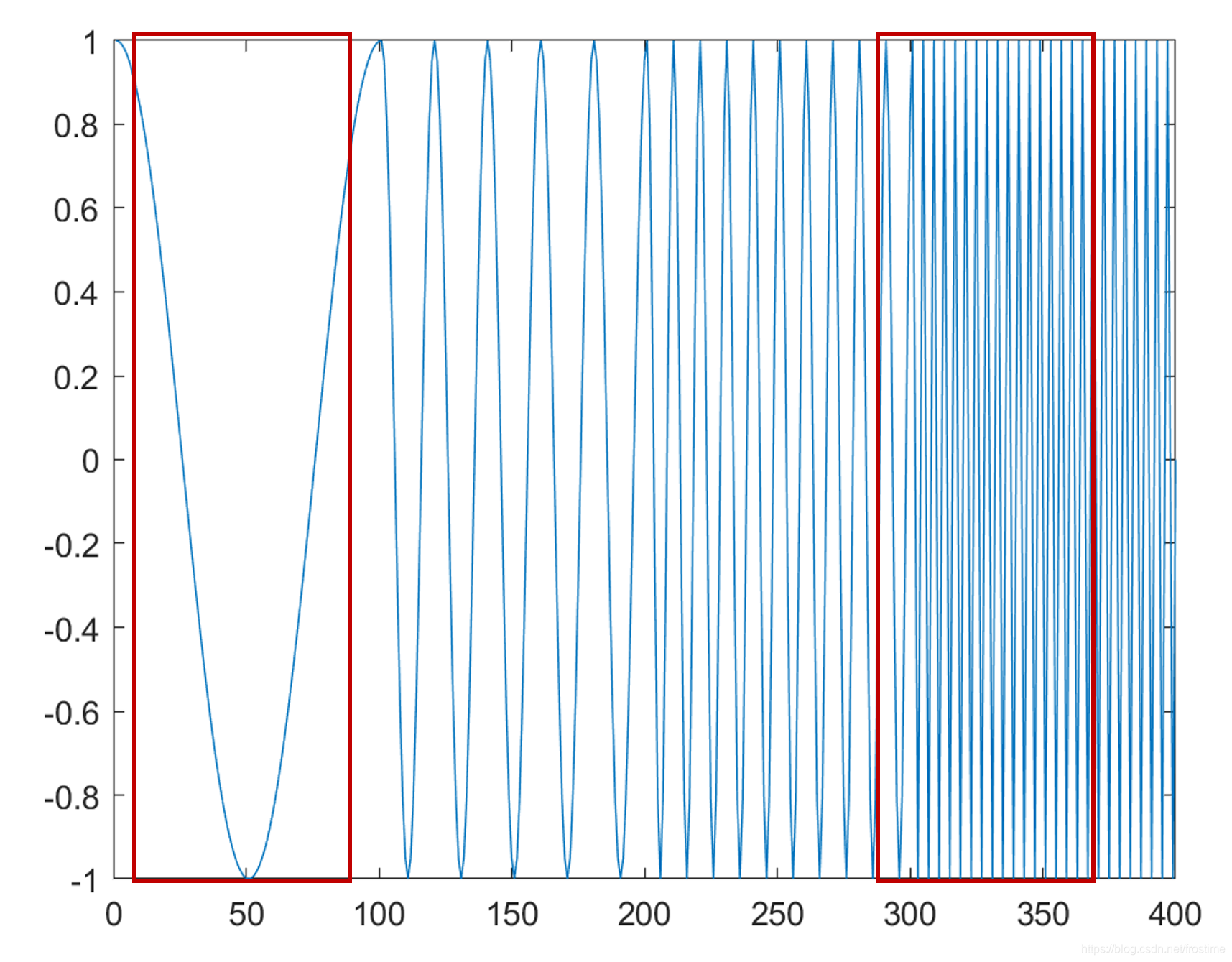
考察一个普普通通的信号:
1 | fs = 1000; |
同样绘制它的时域以及频域图像:
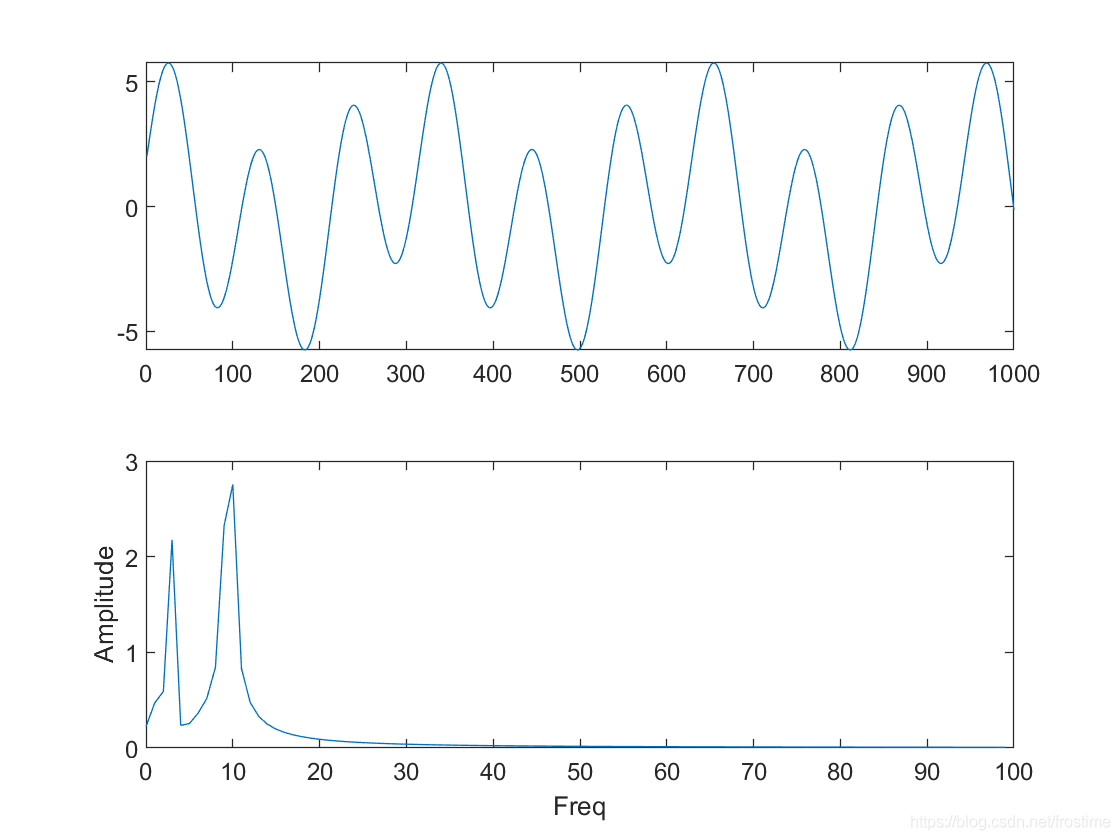
现在给信号加入一个高频突变:
1 | sharp = zeros(1, length(x)); |
然后绘图:
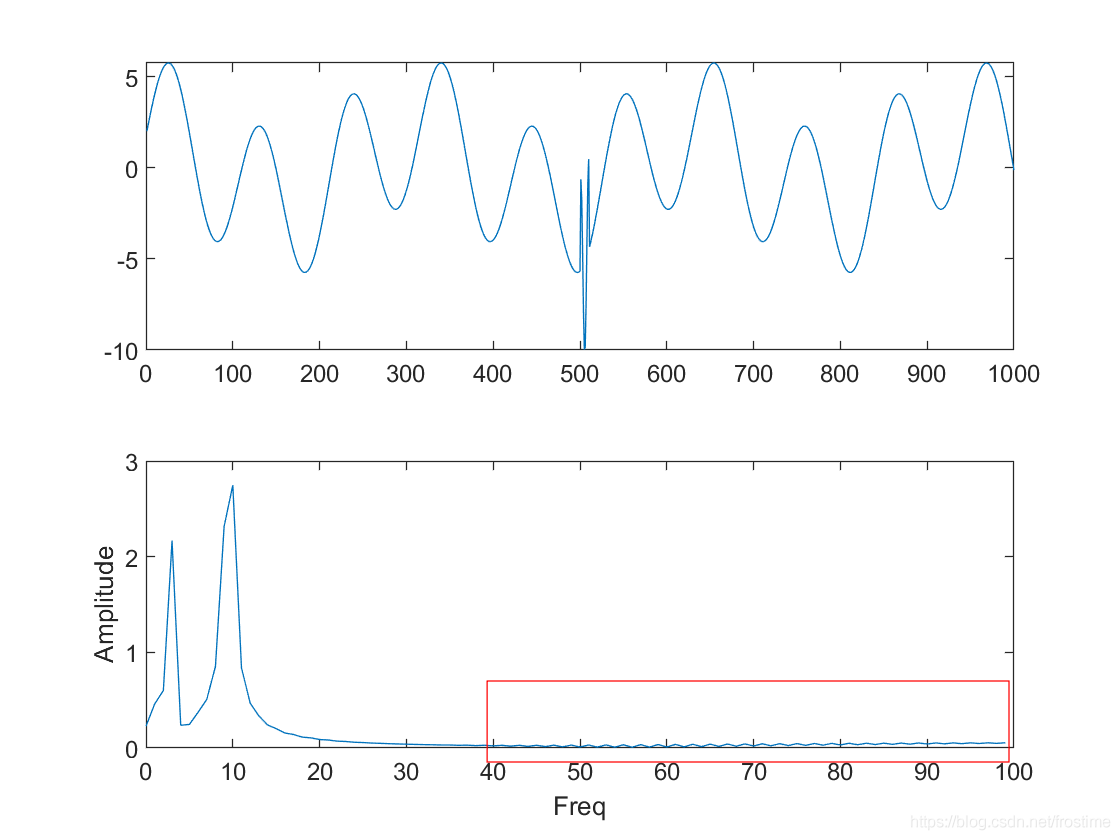
对比两个信号的时域图,我们能很明显发现在第二个信号中央的部分出现了一个突变扰动。然而在频域图中,这样的变化并没有很好的被捕捉到。注意到红框中部分,显然傅里叶变换把突变解释为了一系列低成分的高频信号的叠加,并没有很好的反应突变扰动给信号带来的变化。
为什么我们需要时频分析
通过以上的两个例子,我们不难发现傅立叶变换的缺陷。
第一个例子告诉我们,傅里叶变换只能获取一段信号总体上包含哪些频率的成分,但是对各成分出现的时刻并无所知。因此时域相差很大的两个信号,可能频谱图一样。
第二个例子告诉我们,对于信号中的突变,傅里叶变换很难及时捕捉。而在有些场合,这样的突变往往是十分重要的。
当然如果非要硬杠,也不是完全没办法——这就需要需分析相位谱了,但在实际应用中,有谁会不嫌麻烦地去看相位谱呢?
总而言之,傅里叶变换非常擅长分析那些频率特征均一稳定的平稳信号。但是对于非平稳信号,傅立叶变换只能告诉我们信号当中有哪些频率成分——而这对我们来讲显然是不够的。我们还想知道各个成分出现的时间。知道信号频率随时间变化的情况,各个时刻的瞬时频率及其幅值——这也就是时频分析(引用自知乎)。
所谓时频分析,就是既要考虑到频率特征,又要考虑到时间序列变化。常用的有两种方法:短时傅里叶变化,以及小波变换。本文我们只介绍短时傅里叶变换
2. 短时傅里叶变换原理
短时傅里叶变换的思路非常直观:既然对整个序列做 FFT 会丢失时间信息,那我一段一段地做 FFT 不就行了嘛!这也正是短时傅里叶变换名称的来源,Short Time Fourier Transorm,这里的 Short Time 就是指对一小段序列做 FFT。
那么怎么一段一段处理呢?直接截取信号的一段来做 FFT 吗?一般我们通过加窗的方法来截取信号的片段。定义一个窗函数 $w (t)$,比如这样。
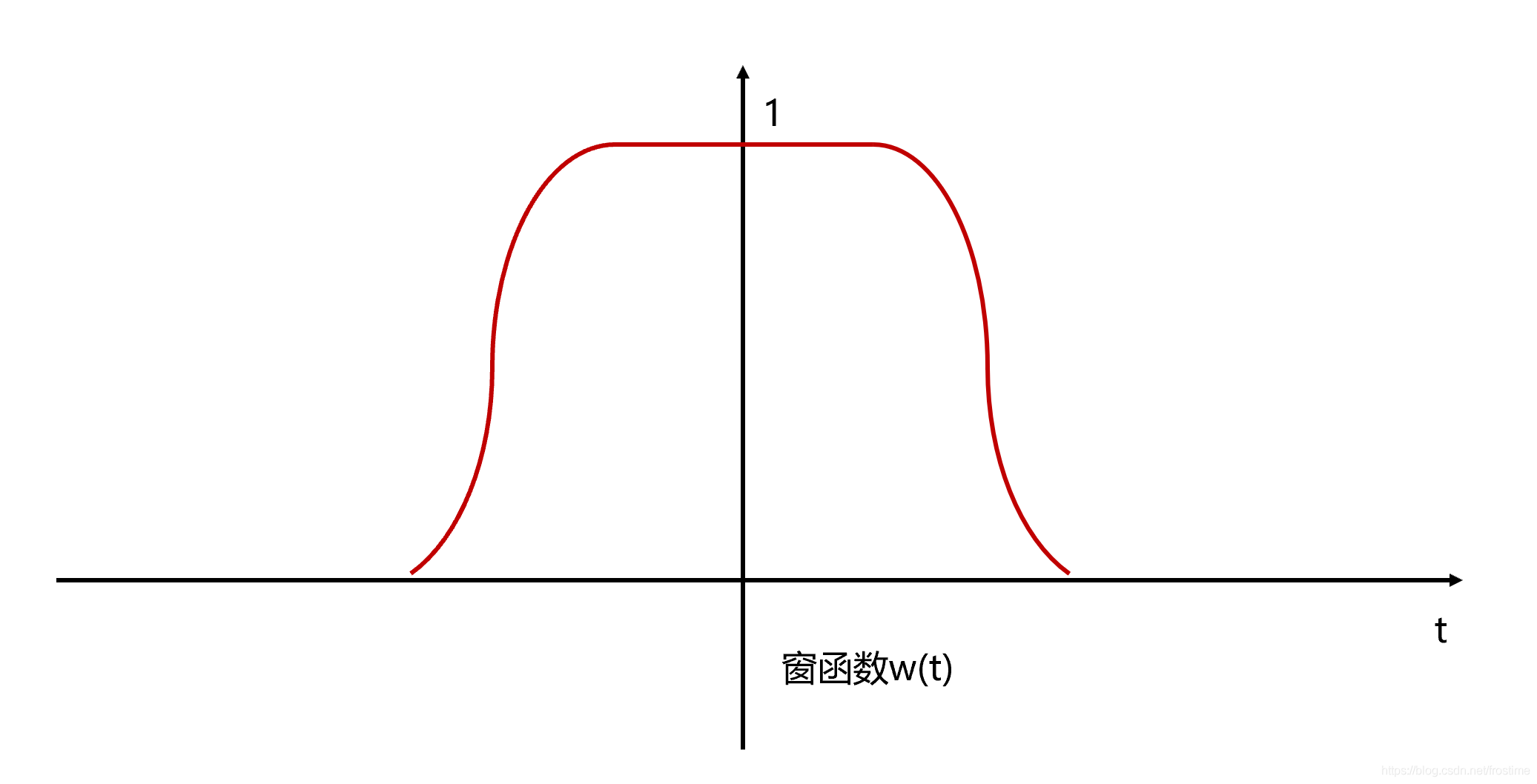
将窗函数位移到某一中心点 $\tau$,再将窗函数和原始信号相乘就可以得到截取后的信号 $y(t)$。
$$
y(t) = x(t) \cdot \textrm{w}(t - \tau)
$$
前面提到的直接截取的方法其实就是对信号加一个矩形窗,不过一般我们很少选用矩形窗,因为矩形窗简单粗暴的截断方法会产生的频谱泄露以及吉布斯现象,不利于频谱分析。更多关于窗函数的内容,可以看这里:加窗法。
对原始信号 $x(t)$ 做 STFT 的步骤如下。
首先将将窗口移动到信号的开端位置,此时窗函数的中心位置在 $t = \tau_0$ 处,对信号加窗处理
$$
y(t) = x(t) \cdot \textrm{w}(t - \tau_0)
$$
然后进行傅里叶变换
$$
X(\omega) = \mathcal{F}(y(t)) = \int_{\infty}^{+\infty}x(t)\cdot \textrm{w}(t-\tau_0) e^{-j\omega t}dt
$$
由此得到第一个分段序列的频谱分布 $X(\omega)$。在现实应用中,由于信号是离散的点序列,所以我们得到的是频谱序列 $X[N]$。
为了便于表示,我们在这里定义函数 $S(\omega, \tau)$,它表示,在窗函数中心为 $\tau$ 时,对原函数进行变换后的频谱结果 $X(\omega)$,即:
$$
S(\omega, \tau) = \mathcal{F}(x(t)\cdot \textrm{w}(t-\tau)) = \int_{\infty}^{+\infty}x(t)\cdot \textrm{w}(t-\tau) e^{-j\omega t}dt
$$
对应到离散场景中, $S[\omega, \tau]$ 就是一个二维矩阵,每一列代表了在不同位置对信号加窗,对得到的分段进行傅里叶变换后的结果序列。
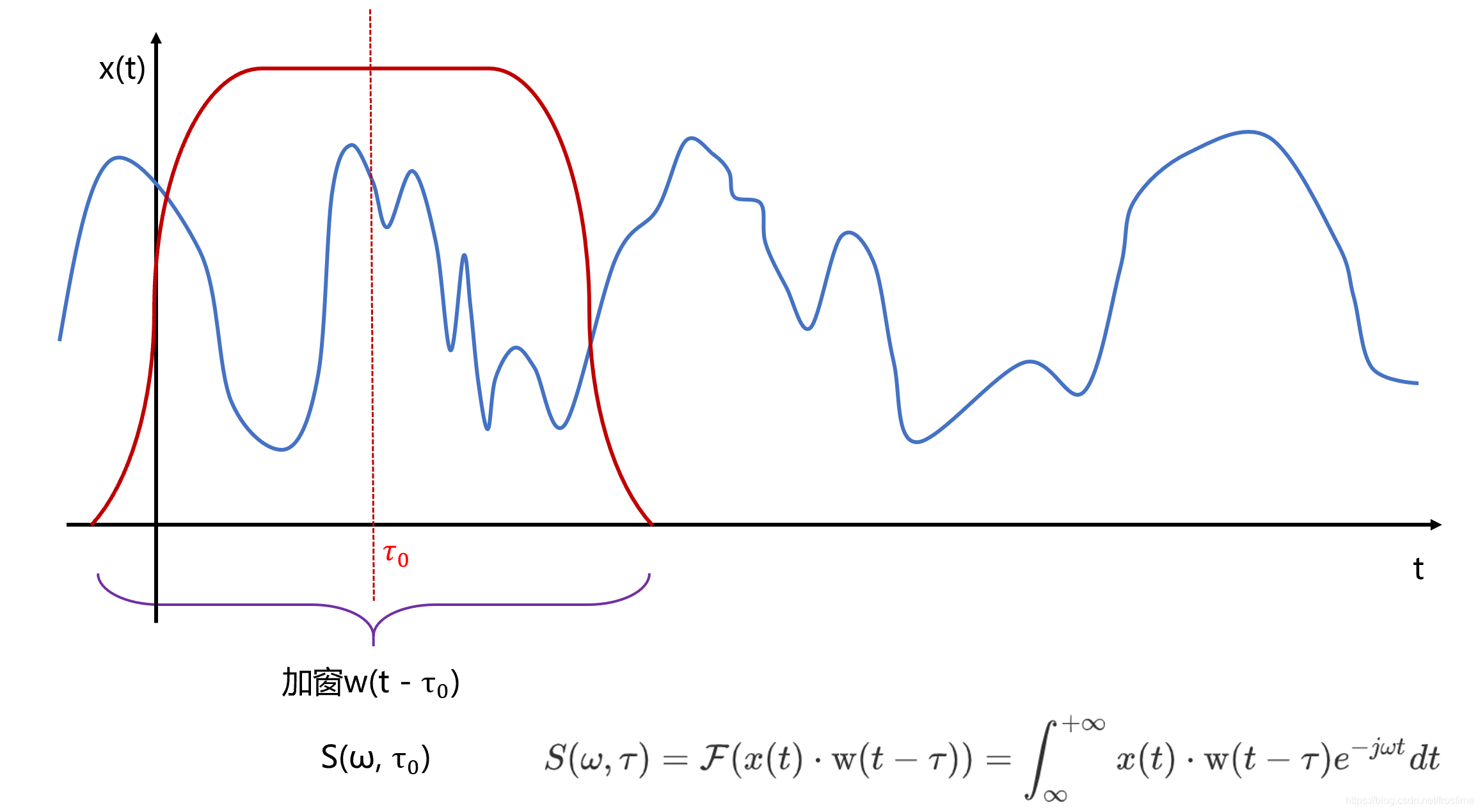
完成了对第一个分段的 FFT 操作后,移动窗函数到 $\tau_1$。把窗体移动的距离称为 Hop Size。移动距离一般小于窗口的宽度,从而保证前后两个窗口之间存在一定重叠部分,我们管这个重叠叫 Overlap。
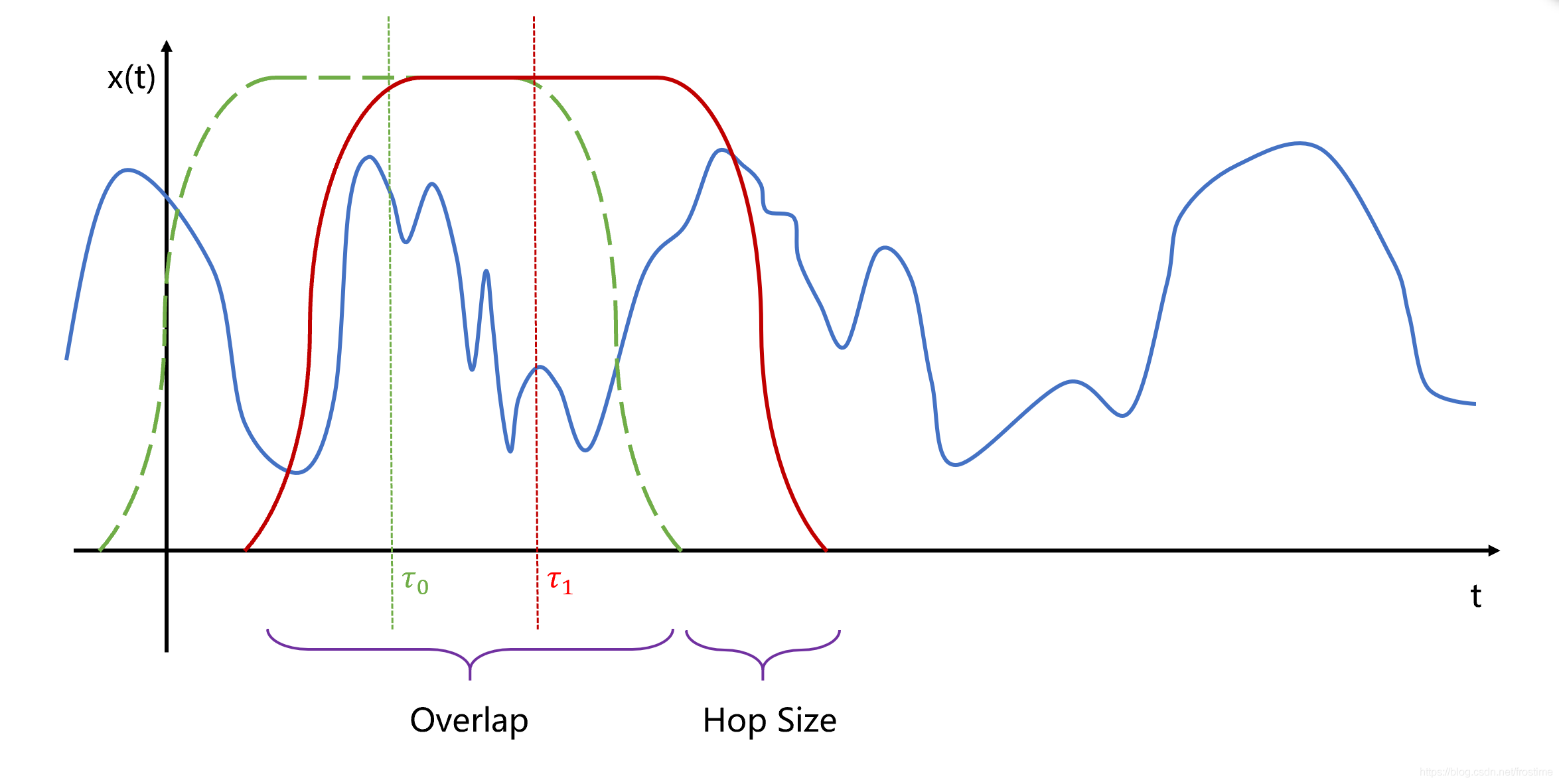
重复以上操作,不断滑动窗口、FFT,最终得到从 $\tau_0 \sim \tau_N$ 上所有分段的频谱结果:
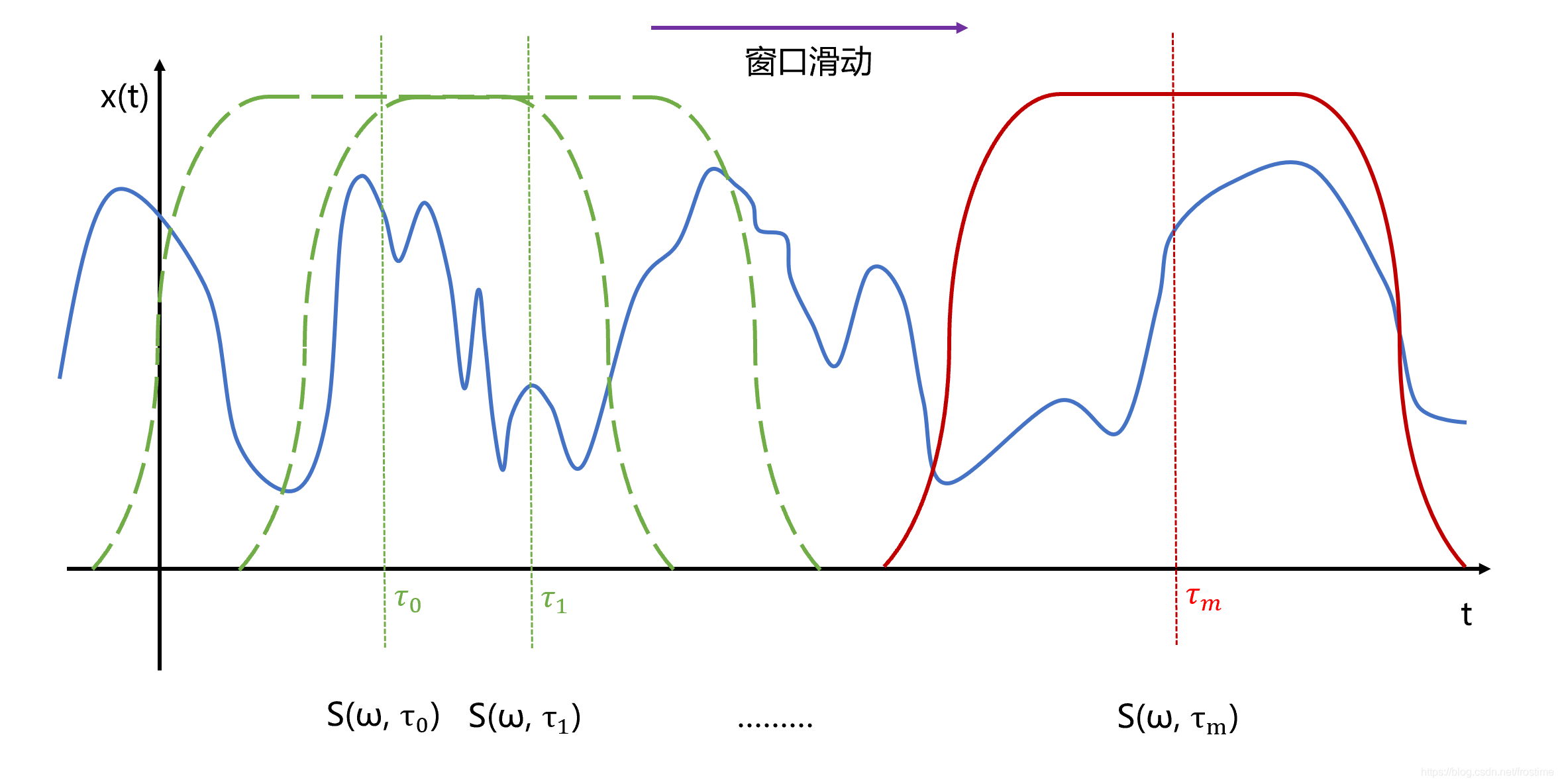
最终我们得到的 $S$,就是 STFT 变换后的结果。
3. STFT 实现
以下代码基于 Matlab 2019b。
3.1 算法实现
STFT 的实现如下,算法返回的三个参数:
- f: m 维向量,表示傅里叶变换后每个点对应的频率值,单位为 Hz
- t: n 维向量,表示 n 个窗口中心时间 $\tau_1 \sim \tau_n$,单位为秒
- STFT: 一个二维矩阵 $[m, n]$,每个列向量代表了在对应 $\tau$ 上 FFT 变换的结果
1 | function [STFT, f, t] = mystft(x, win, hop, nfft, fs) |
3.2 使用范例
我们这里使用 Case 1 的范例来看看 STFT 效果如何。
为了方便可视化,这里给出了对 STFT 变换后的可视化函数。
1 | function PlotSTFT(T,F,S) |
注意上面这个函数依赖于 signalwavelet 包,如果没有这个依赖的话,我还提供了一个粗糙版的绘图函数,用法基本类似,不过最后一个参数需要把从窗函数对象传进去:
1 | function PlotSTFT_2(T, F, S, win) |
对 Case 1 中的两种情况进行分析,代码如下
1 | close all; clear; clc; |
可以看到,在 FFT 中无法区分的频谱图像在 STFT 中区分就非常明显,可以看出按照不同的时间分段,频谱分布的变化。
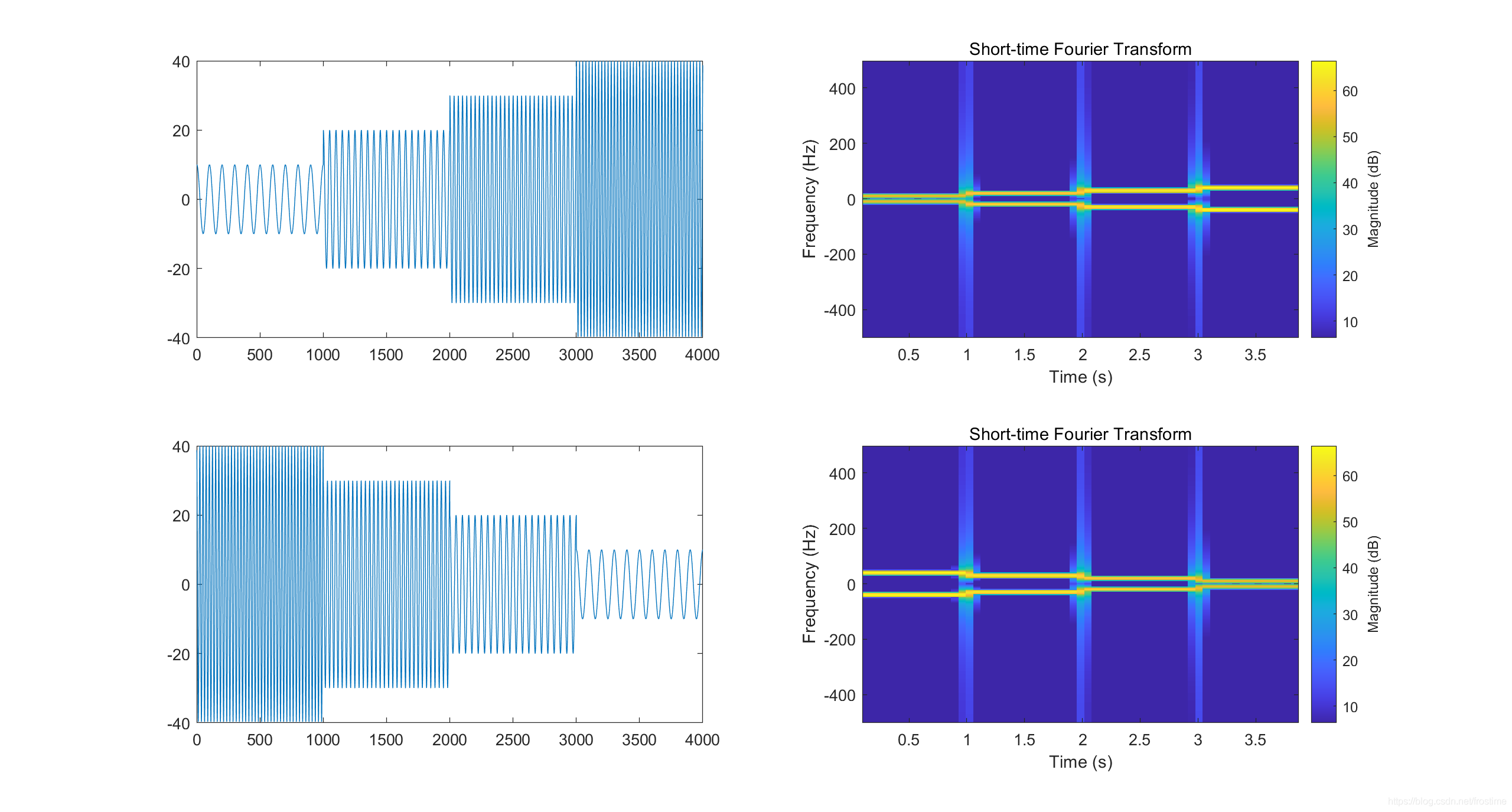
为了更好地理解,将右上角的图做一次三维旋转:
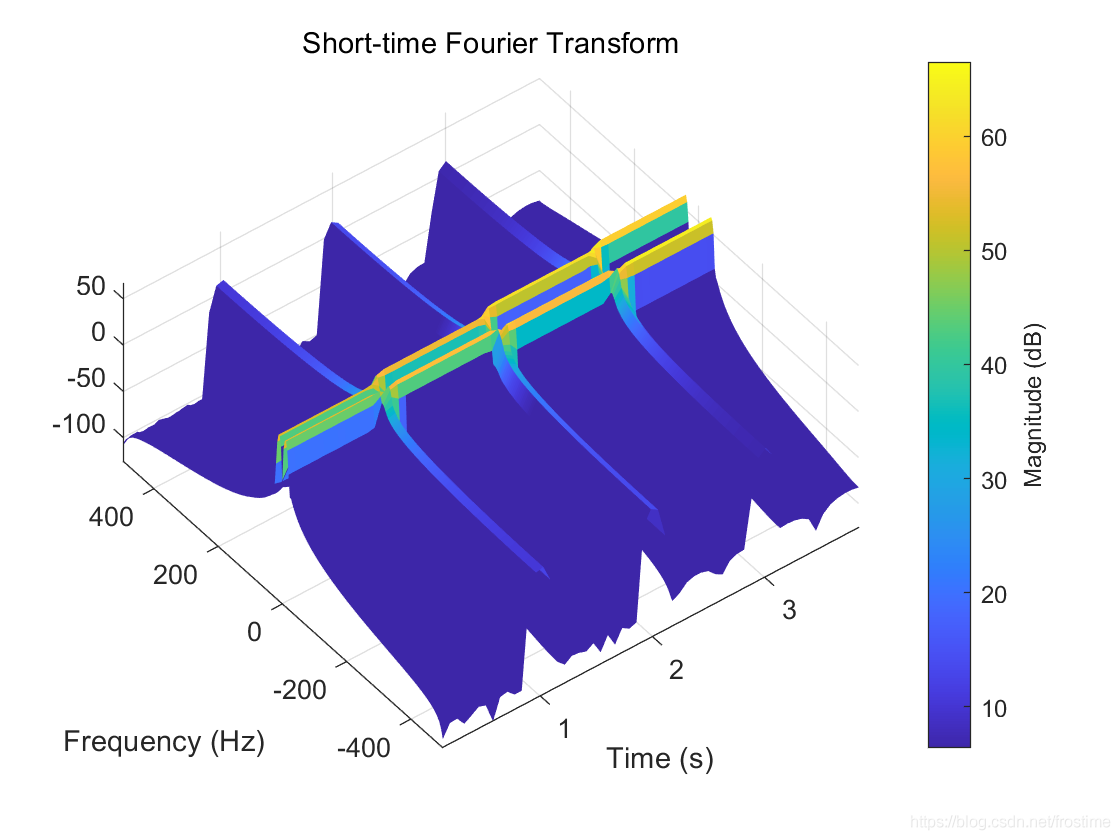
可以非常清晰地看出频率分布随时间的变换。注意到分界线处存在异常的高频成分(就是 STFT 图像中那三条竖线),这是因为时域信号突变导致的高频成分。
3.3 Matlab 中的实现
在老的版本中,Matlab 中 STFT 的函数名为 spectrogram,而在 2019 版本中,引入了新的函数 stft,用法和我上面的实现的程序基本一致。
1 | close all; clear; clc; |
需要注意的是,我实现的时候用的参数是 hop size,而 matlab 提供的函数需要的参数是 overlap 这个别搞混了。结果如下。
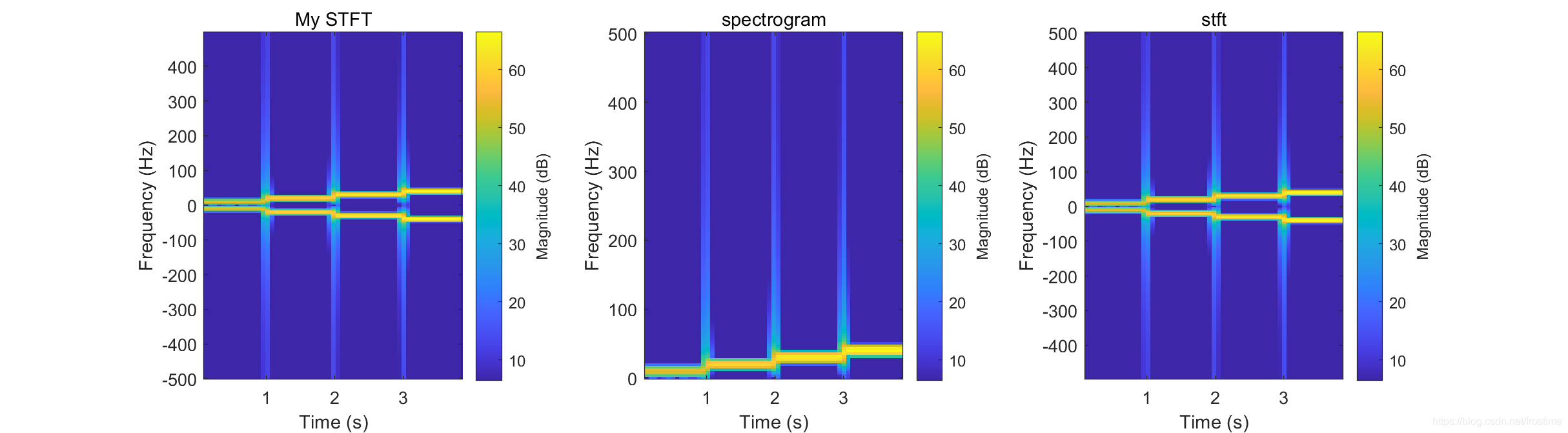
要注意的是,spectrogram 输出的是单边谱,而 stft 输出的是双边谱,其他区别倒不大。但是 spectrogram 还可以输出功率谱,而 stft 就不行了。
4. STFT 的缺点
如果你仔细分析上面的内容,你会发现短时傅立叶变换也有不容忽视的缺陷。
最明显的一个问题:窗口的宽度该设多少为好呢?为了阐明这个问题的影响,我们做这么一个实验:调整不同 wlen 的值,来看看影响。
1 | len = [32, 64, 128, 256]; |
结果如下:
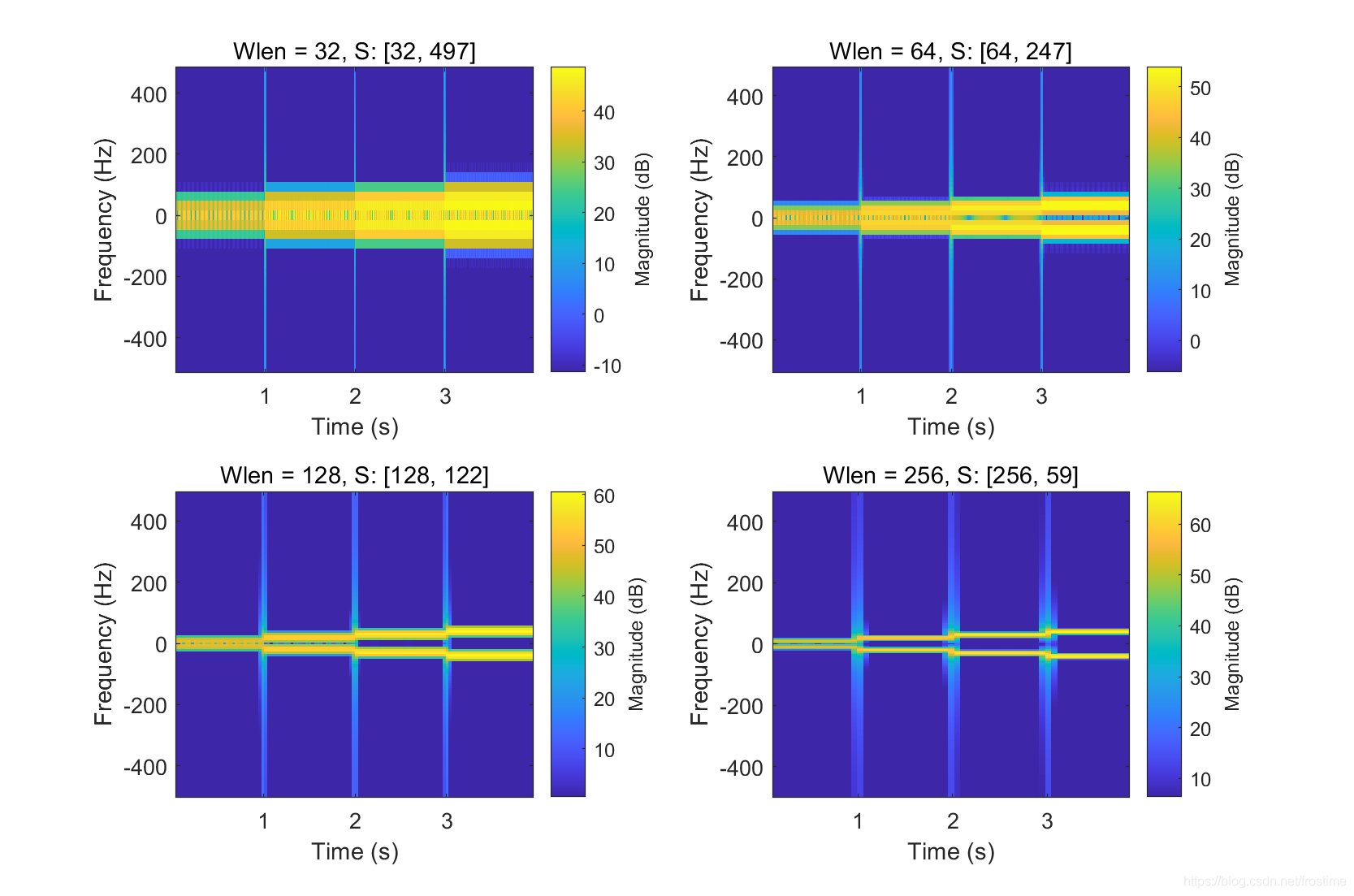
注意 S 的尺寸随 wlen 的变换,不难发现一个事实:
- 窗太窄,窗内的信号太短,会导致频率分析不够精准,频率分辨率差,具体表现是黄色的横线越来越宽、越来越模糊
- 窗太宽,时域上又不够精细,时间分辨率低,具体表现是淡蓝色的竖线越来越宽、越来越模糊(还记得吗,竖线表示交界处的突变造成的高频干扰成分)
从定量的角度来看,STFT 的时间分辨率取决于滑移宽度 $H$,而频率分辨率则取决于 $\frac{F_s}{H}$。显然,一方的增加必然意味着另一方的减小。这就是所谓的时频测不准原理(跟海森堡测不准是一个性质),具体关系为:
$$
\Delta t \cdot \Delta f \geqslant \frac{1}{4\pi} $$
另外,固定的窗口大小过于死板。对低频信号而言,有可能连一个周期都不能覆盖;对高频信号而言,可能覆盖过多周期,不能反映信号变化。
也就是说,这又是一个 Trade-Off 问题,而一个问题一旦进入 Trade-Off 模式,就开始变得玄学起来了。
为了打破这种玄学困境,就需要一个更加强大的武器——小波变换。
至于小波变换,那就是另一个故事了。
都看到这儿了,不如关注每日推送的“科文路”、互动起来~
时频分析——短时傅里叶变换STFT