支持向量机SVM（上）——分类

文章来自微信公众号“科文路”，欢迎关注、互动。转发须注明出处。

本系列文章主题为“备查手册”，旨在帮助读者快速回忆起相关技术细节。SVM 系列，按应用预计分为三个部分：分类、回归和单分类

本文内容主要源自 A Practical Guide to Support Vector Classification，介绍 SVM 用作分类算法的原理、可使结果更好的工作流程。

用途

使用训练数据训练产生一个模型，用于在新的数据上预测类别

The goal of SVM is to produce a model (based on the training data) which predicts the target values of the test data given only the test data attributes.

含义

支持向量机的学习策略就是间隔最大化，可形式化为一个求解凸二次规划(convex quadratic programming)的问题，也等价于正则化的合页损失函数的最小化问题。支持向量机的学习算法是求解凸二次规划的最优化算法。——《统计学习方法》,李航

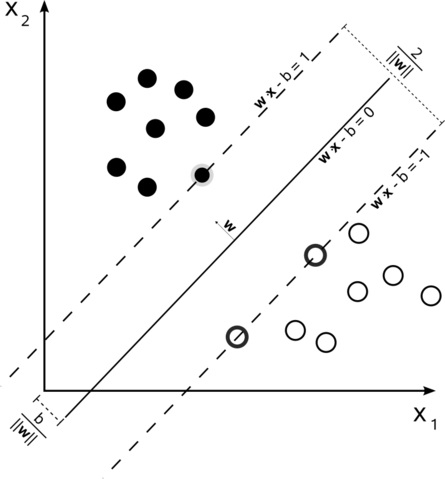
上图来自维基百科“支持向量机”

Given a training set of instance-label pairs $(\mathbf{x}_i, y_i), i=1,\cdots,l$, where $\mathbf{x}_i \in \mathbb{R}^n$ and $y_i \in {1,-1}^l$, the support vector machines (SVM) (Boser et al., 1992; Cortes and Vapnik, 1995) require the solution of the following optimization problem:

$$
\begin{array}{c}
\min {\mathbf{w}, b, \xi} \frac{1}{2} \mathbf{w}^{T} \mathbf{w}+C \sum{i=1}^{l} \xi_{i} \
\text { subject to } y_{i}\left(\mathbf{w}^{T} \phi\left(\mathbf{x}{i}\right)+b\right) \geq 1-\xi{i} \
\xi_{i} \geq 0
\end{array}
$$

面试常考：$C$ 的作用是什么？$\phi$ 的含义是什么？如何使用 SVM 解决多分类问题？

核技巧

SVM 在 $\mathbf{x}_i$ 通过 $\phi$ 被映射到的高维空间中寻找一个最大间隔线性可分超平面。

通过核技巧可以简化计算，常用核函数（$K\left(\mathbf{x}{i}, \mathbf{x}{j}\right)=\phi(\mathbf{x}{i})^\top\phi(\mathbf{x}{j})$）包括：

• Linear, $K\left(\mathbf{x}{i}, \mathbf{x}{j}\right)=\mathbf{x}{i}^{T} \mathbf{x}{j}$
• Polynomial, $K\left(\mathbf{x}{i}, \mathbf{x}{j}\right)=\left(\gamma \mathbf{x}{i}{ }^{T} \mathbf{x}{j}+r\right)^{d}, \gamma>0$
• RBF, radial basis function, $K\left(\mathbf{x}{i}, \mathbf{x}{j}\right)=\exp \left(-\gamma\Vert\mathbf{x}{i}-\mathbf{x}{j}\Vert^{2}\right), \gamma>0$
• Sigmoid, $K\left(\mathbf{x}{i}, \mathbf{x}{j}\right)=\tanh \left(\gamma \mathbf{x}{i}{ }^{T} \mathbf{x}{j}+r\right)$

推荐工作流程

可大幅提高 accuracy

• Transform data to the format of an SVM package
• Conduct simple scaling on the data
• Consider the RBF kernel $K(\mathbf{x}{i}, \mathbf{x}{j})=e^{-\gamma\Vert\mathbf{x}{i}-\mathbf{x}{j}\Vert^{2}}, \gamma>0$
• Use cross-validation to find the best parameter $C$ and $\gamma$
• Use the best parameter $C$ and $\gamma$ to train the whole training set
• Test

都看到这儿了，不如关注每日推送的“科文路”、互动起来~