文章来自微信公众号“科文路”，欢迎关注、互动。转发须注明出处。
谢邀，本人五套房，两套广州，两套佛山，一套惠州，除了佛山其中一套是底商外，其他都是住宅。
为什么不卖掉一套实现财务自由？因为本来持有它们就是实现财务自由了，或者说是因为持有资产才实现财务自由，我就拿广州其中一套来说吧
文章来自微信公众号“科文路”，欢迎关注、互动。转发须注明出处。
通常，一个省级行政区内最有名的文物都会被收藏到其省博物馆内。所以，”省馆之宝”系列将介绍我国各个省馆的明星文物。每周二更新，本文为第 11 期。
本期介绍山东博物馆官网主页提到的十大镇馆之宝。本期内容全部来自山东博物馆：官网，更多细节请访问官网。
值得一提的是，该博物馆官网是目前已更新系列文章的博物馆中，唯一一个提供了公众版/少儿版两种版面的官网。
但遗憾的是，该网页提供的 3D 浏览功能在目前被广泛使用的类 Chrome 浏览器（Edge等）上并不支持。
文章来自微信公众号“科文路”，欢迎关注、互动。转发须注明出处。
科普：地震发生，室内避险指南
2022年9月5日12时52分，四川省甘孜州泸定县发生6.8级地震，震源深度16公里。
本文内容整理自 国家减灾网
首先，不要慌！
生死有命，把能做的做好。
简单讲就两点：
- 跑的快的，赶紧跑，不跑也把大门先打开；
- 跑不了的，找个牢靠的位置躲下边，保护好头部。有机会了再跑！
文章来自微信公众号“科文路”，欢迎关注、互动。转发须注明出处。
一周速览为每周日晚固定栏目，将会回顾本周的热点事件。
本周发布回顾
- 科技：卡尔曼滤波器 原创
- 省馆之宝：江西，江南青铜王国
- 逛知乎：国防科技大学非军籍研究生是什么体验？
- MLIR：静态单赋值，SSA 原创
- 荐歌：各自远扬（中孝介），隐形纪念（丹增尼玛）
- 生活：李诞，救猫还是救画？
文章来自微信公众号“科文路”，欢迎关注、互动。转发须注明出处。
这两天把这周的《脱口秀大会》补上了。还是不错的，至少有 1/4 的段子都能让我很开心。
注意到其中一位选手的段子中打趣说，李诞的脱口秀也就那样。
文章来自微信公众号“科文路”，欢迎关注、互动。转发须注明出处。
周末愉快！
虽然说是周末愉快，但其实自打昨天以来，成都开始居家办公，所以其实我已经在家两天了。在家的生活也并不如想象，因为毕竟还是有一堆工作要做的，进度又不因为疫情等待。
今晚有李健的线上音乐会。
文章来自微信公众号“科文路”，欢迎关注、互动。转发须注明出处。
Multi-Level Intermediate Representation（MLIR）是创建可重用、可扩展编译器基础设施的新途径。本文为 MLIR 系列第 2 期，介绍基础概念 SSA。
文章来自微信公众号“科文路”，欢迎关注、互动。转发须注明出处。
科文路注：非军籍生，顾名思义，不具有军籍生的军人待遇。需要自行缴纳各种费用。另外录取和分配程序类似于普通大学学生。
实话实说，我是之前17级国防科大计算机专业研究生毕业的。基本我这一届非jun都去了大厂，华为，腾讯，百度，字节，京东等等，华为最多，大家过得都不错。我自己在初创、字节都呆过，目前在初创做研发。
文章来自微信公众号“科文路”，欢迎关注、互动。转发须注明出处。
通常，一个省级行政区内最有名的文物都会被收藏到其省博物馆内。所以，”省馆之宝”系列将介绍我国各个省馆的明星文物。每周二更新，本文为第 10 期。
本期介绍江西省博物馆的馆藏代表，包括一件禁止出国（境）展览文物以及几件博物馆典藏精品。本期内容全部来自江西省博物馆：官网，更多细节请访问官网。
另外，江西省博物馆的官网上有下面文物的 3D 展示，能看到比静态搁置的现场更多的细节，有把玩感： http://www.jxmuseum.cn/collection/jpxs?page=1
哈哈，还有个有意思的，这儿有个地名叫新干县大洋洲。
已收录至https://zhuanlan.zhihu.com/p/52815498
本文内容来自官方教程
可以直接跳到6看
0 例
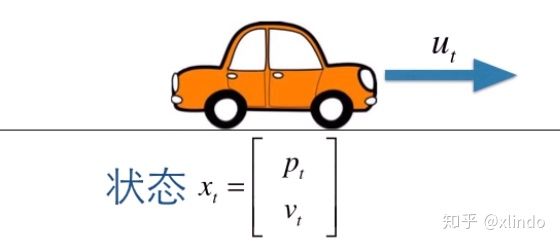
可以列出模型
$$\begin{cases} p_t = p_{t-1}+ v_{t-1} \times \Delta t+u_t\times\frac{\Delta t^2}{2} \ v_t=v_{t-1}+u_t\times\Delta t\end{cases} $$
则可以写出状态空间方程
$$\left[\begin{matrix}p_t \ v_t\end{matrix}\right]=\left[\begin{matrix}1 & \Delta t \ 0 & 1\end{matrix}\right]\left[\begin{matrix}p_{t-1} \ v_{t-1}\end{matrix}\right]+\left[\begin{matrix}\frac{\Delta t^2}{2} \ \Delta t\end{matrix}\right]u_t $$